
We thought about the problem a bit, but couldn't recall any formulas for a circle that didn't require one to know the radius, diameter, or circumference as terms of the equation. I did remember that the solution involved making two right triangles along the arc. While eating my peanut butter sandwich, I decided that I could use the two right triangles to get a quick and dirty solution. I knew I could draw the two triangles at scale and cut them out. Then I could use a set of circles drawn at the same scale and slide the triangles over the concentric circles until I found the best fit. This sort of the way we calculate the rim diameters of ceramic fragments.
We all knew that our math friends would remember the equations, however.
Pete and Mark Dice phoned in an answer. Pete promised to send me his figures by email.
C. Crosse commented on the blog. She said, "Given that c is a straight line between two points on the circumference of a circle--X and Z--which is called the cord, the curved line would be called arc XZ. Assuming you know c (not XZ) and m--the height of the arc created by the chord--then the formula would be:
r = (m² + ¼c²)/2mPete Foss made a comment on the project Facebook page:
that says your kiln was 1.88 meters in radius. 12 feet in diameter."
He added, "Hooray for Google!"
Indeed. The page that Pete sent includes a useful illustration:
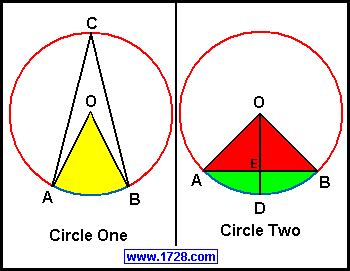
I'd still like to hear from one of my friends that are math teachers! We have marked out a circle of 12 feet on the ground surface. As we excavate more of the kiln, we will be able to get more accurate measurements. Family oral history said that the kilns were "about 14 feet across" and that there may be three or four of them all in the back yard. We'll see what we find out.
May 28, 2009- update.
I have heard from my friend Kristin Z. Cook, who teaches math at a high school in Milwaukee. She ran the numbers and said: "I am assuming the perpendicular segment you drew bisects the 1.8-meter segment. If that is the case, then I calculated the radius to be approximately 1.8759 m, the diameter to be 3.7517 m, and the circumference to be 11.7864 m." She promised to scan and email me her a page that showed her work. She is a math teacher, after all!
My colleague Steve Walton also worked up a solution, but not to be outdone by others, he formatted a diagram and included it in his email:

So there is pretty wide agreement that the kiln is between 12 and 12.5 feet in diameter. Pretty close to the 14 feet diameter recorded in oral histories and given the inaccuracies of our measurements, we need to leave a little wiggle room in our conclusions.
If you are curious, here is how I figured out my estimate. I drew copies of sets of right triangles using a scale. The right triangles split the chord evenly in half. I new that I could make a second set of overlapping triangles on a second overlapping chord, then line up both sets on a scale drawing. If I projected their short side as in the drawing below, I knew they would intersect in the middle of the circle and allow me to measure the radius! I always liked geometry proofs more than algebraic ones....

I've emailed you with a jpg of the derived equations. First principles, my friend!
ReplyDelete